Using inverse transform sampling to generate random numbers in a given distribution

In inverse transform sampling, we use the inverse cumulative distribution function (CDF) to generate random numbers in a given distribution. But why does this work?

This post attempts to demystify inverse transform sampling works by plugging samples from a distribution into the same distribution’s CDF and verifying that we get numbers with a uniform distribution in \([0, 1]\).

Let’s start with a few definitions first.

Definitions

We want to generate random numbers according to a given probability density function (PDF) \(f(x)\). The probability density function \(f(x)\) and the cumulative distribution function \(F(x)\) are related to each other by an integral:

$$ F(x) = \int f(x) dx $$

We can use this to calculate the CDF of a simple function, the uniform density function U in the interval \([0,1]\). In U, the probability density is constant everywhere in the interval:

$$ F_U(x) = \int cdx = cx+d $$

The cumulative distribution function has the property that it must be zero before the range, and one after the range. We can use these constraints, \(U(0)=0\) and \(U(1)=1\), to obtain

$$ F_U(x) = x. $$

The CDF of a sample is uniformly distributed

Inverse transform sampling works, because when we plug values of random variable \(X\) into its own CDF \(F_X\), we obtain numbers which are uniformly distributed in \([0, 1]\). I.e., the shape of \(F_X(X)\) is uniform.

Let’s observe the distribution we obtain from the normal distribution’s CDF over normally distributed random numbers. This is easy to do with Python and a few libraries.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

import matplotlib.pyplot as plt
import numpy as np
import math

rng = np.random.default_rng()

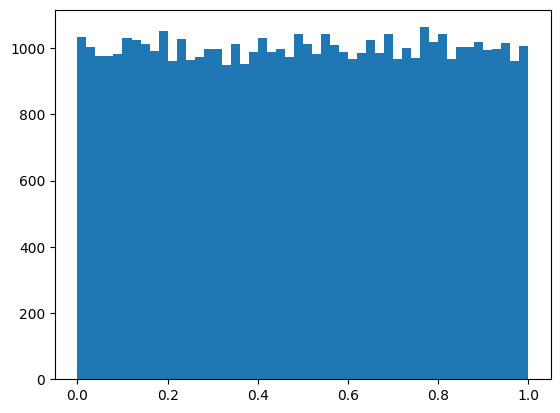
# The definition of the normal distribution's CDF which we will reuse
cdf_normal = lambda x : 0.5 * (1.0 + math.erf(0.7071067811865475 * x))

n = rng.normal(loc=0.0, scale=1.0, size=50000)
x = np.array([cdf_normal(x) for x in n])
plt.hist(x, bins=50)

normal distribution

From the histogram we can see that \(F_N(N)\) yields nice uniformly distributed values between 0 and 1.

Using the definition of the CDF,

$$ F_X(x) = P(X \le x), $$

we also arrive at the conclusion that the distribution of \(F_X(X)\) is uniform. Let’s assign \(Z = F_X(X)\) and use the definition of the CDF on it:

$$ F_Z(x) = P(F_X(X) \le x) = P(F^{-1}_{X}(F_X(X)) \le F_X^{-1}(x)) = P(X \le F_X^{-1}(x)) $$

$$ \therefore F_Z(x) = F_X(F_X^{-1}(x)) = x $$

The shape of \(F_Z\) is that of the uniform distribution \(F_U\) that we calculated earlier! This is why for \(X\), our random number with a distribution, we can do this:

$$ F_X(X) = (\textrm{uniformly distributed number}) $$

$$ \therefore X = F^{-1}(\textrm{uniformly distributed number}). $$

Generating random numbers using inverse transform sampling

We can now generate random numbers in the shape of any given density function using the recipe:

  1. Given a PDF, calculate the CDF using the integral equation.
  2. Take the inverse of the CDF.
  3. Plug your uniformly distributed random numbers into the inverse CDF.

For example, to generate random numbers according to the density function \(f(x)=x^2\), in the range \([0,2]\), we can apply the recipe as follows.

First, we obtain the CDF.

$$ F(x) = \int x^2dx = C \frac{x^3}{3} $$

Using the constraints \(F(0)=0\) and \(F(2)=1\), we get

$$ F(x) = \frac{1}{8}x^3. $$

Next, let’s take the inverse of \(F(x)\):

$$ F^{-1}(x) = (8x)^{\frac{1}{3}} $$

Finally, we can plug numbers into our inverse function.

1
2
3

u = rng.uniform(0, 1, 50000)
x = np.array([(8.0 * x) ** (1.0 / 3.0) for x in u])
plt.hist(x, bins=50)

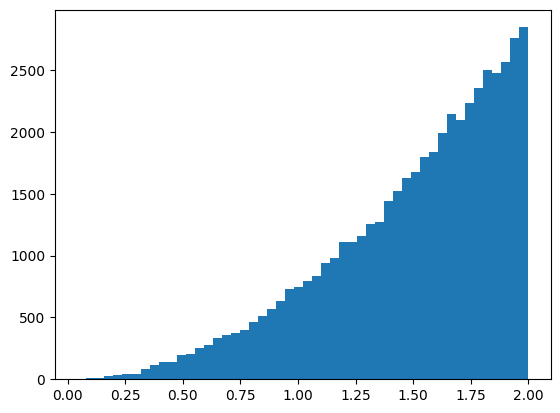
power distribution

To confirm that everything works, we can look at a plot of \(x^2\).

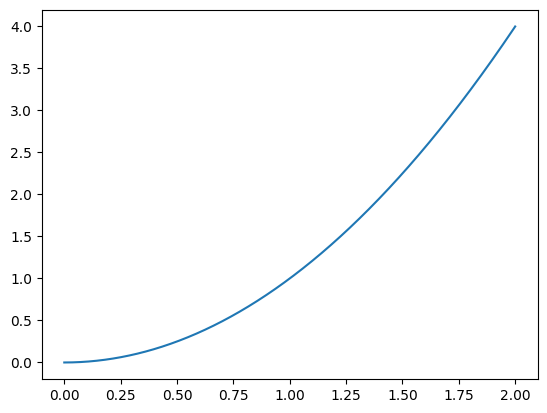
curve

Inverse transform sampling using normally distributed random numbers

The fact that evaluating a uniform distribution function yields uniformly distributed values means that we can actually plug in random numbers from any distribution into \(F^{-1}\)! Given that two CDFs \(F(X)\) and \(G(Y)\) have the exact same uniform distribution, we can apply the inverse of \(F^{-1}\) like we did before to find the mapping between \(X\) and \(Y\):

$$ F(X) = G(Y) $$

$$ \therefore X = F^{-1}(G(Y)) $$

We can use this fact to generate random numbers in our earlier distribution \(f(x)=x^2\) using normally distributed random numbers:

1
2
3

# Note how `x` is replaced with `cdf_normal(x)` here
x = np.array([(8.0 * cdf_normal(x)) ** (1.0 / 3.0) for x in n])
plt.hist(x, bins=50)

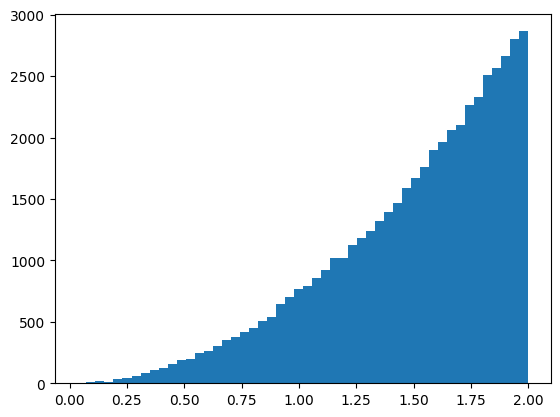
curve

And again, looks like a graph of \(x^2\)!

I’m not sure why you would want to generate random numbers in a given distribution in such a contrived way, but it’s nice to know that it is possible.

Contents