Pathtracing tidbits: integrating animated blue noise

Alan Wolfe’s paper, “Using Blue Noise for Ray Traced Soft Shadows”, presents a great method for reducing the perceived noise in soft shadows. It can be readily adapted to a path tracer as well, where it will yield images with better clarity, even with only a few samples.

Take a look at an image rendered with regular RNG white noise in the left half, and blue noise in the right half:

Using blue noise results in much better clarity even though a lot of noise is still present in this 1spp image!

Adapting the method for a path tracer requires a small modification in order to avoid strange-looking spatial correlations in the noise pattern.

Path tracer adaptations

The method presented in the paper uses a golden ratio low-discrepancy sequence in place of a random number for each frame. Neighboring pixels are spatially decorrelated by adding blue noise to each golden ratio sequence value, to prevent pixels from having an identical noise value each frame.

1
2
3
4

float AnimatedBlueNoise(in float blueNoise, in int frameIndex)
{
    return fract(blueNoise + float(frameIndex % 32) + 0.61803399);
}

2D sequences and noise

Unlike the paper, 2D noise is used here in order to randomly sample a hemisphere. Various golden ratio sequence can be obtained from “The Unreasonable Effectiveness of Quasirandom Sequences”. The pseudocode for the n th term of a 2D golden ratio sequence is defined as

g = 1.32471795724474602596
a1 = 1.0/g
a2 = 1.0/(g*g)
x[n] = (0.5+a1*n) %1 
y[n] = (0.5+a2*n) %1 

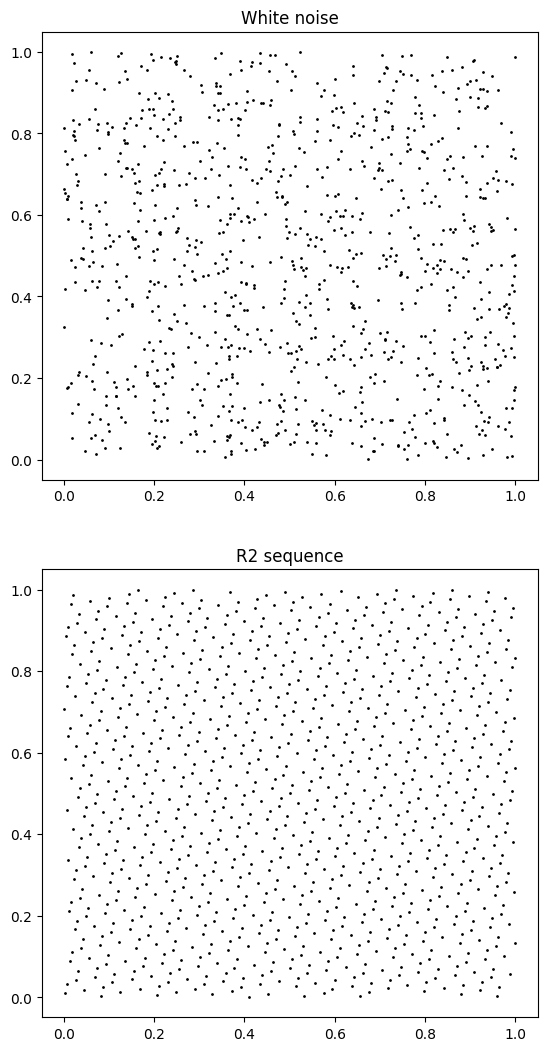
The very regular pattern of this sequence (called the “R2 sequence” in the plot below) can be seen by plotting N values and comparing to white noise.

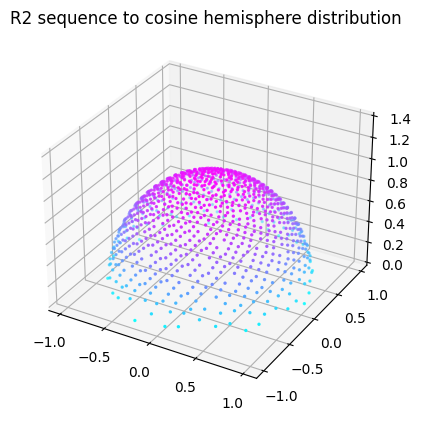
Using the 2D golden ratio sequences values in place of random numbers when sampling a cosine-weighted hemisphere results in a very regular distribution about the hemisphere.

Pre-calculated blue noise values can be downloaded from Moments in Graphics. These blue noise mask textures are tileable, and I found that a 128x128 mask was enough to render images without tiling artifacts.

Putting these together by naively following the paper (i.e. plugging 2D blue noise and the R2 sequence into an equivalent AnimatedBlueNoise function) results in images with a strange unmotivated shadow.

Animating blue noise per bounce

On each ray bounce, a new direction needs to be computed. If the animated blue noise is computed per-frame, per-pixel, we end up reusing the same animated blue noise on each bounce, and thus keep generating the same hemisphere direction for each vertex along the path.

One way of solving this issue is to increment the frame index counter each time animated_blue_noise function is called.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

struct noise_state
{
    float2 value;
    uint   frame_idx;
};

float2 animated_blue_noise(thread noise_state& noise)
{
    float const  n = noise.frame_idx++;
    float const  a1 = 0.7548776662466927f;
    float const  a2 = 0.5698402909980532f;
    float2 const r2 = float2(n * a1, n * a2);
    return fract(noise.value + r2);
}

In this scheme, each bounce consumes a new value in the golden ratio sequence. To prevent consecutive frames from using overlapping golden ratio sequence values, we can initialize the frame index as a multiple of the number of bounces:

1
2
3

float2 const noise_value = // texture lookup...
uint const   noise_frame = (uniforms.frame_idx % 128U) * NUM_BOUNCES;
noise_state  noise = {noise_value, noise_frame};

With these changes in place, the spatially correlated black pixels vanish from the basic 1spp render of cubes: